Mastering Binary Data in JavaScript: ArrayBuffer, TypedArray, and DataView Explained
A Deep Dive into JavaScript’s Powerful Binary Data Structures: ArrayBuffer, TypedArray, and DataView
Often our simple, weakly typed, DOM manipulating JavaScript applications built primarily for smooth user interfaces find themselves in the middle of use cases where they need to handle binary data in some capacity. But isn't that mostly the job of the backend or the middle end, one might wonder - for decently complex software dealing directly with blobs or files, HTTP octet responses, web socket messages from other services, image processing use cases, or transferring data to the GPU, the answer to that question is likely a no. To support these use cases, JavaScript exposes some pretty performant and powerful data structures to handle incoming streams of binary data and model them to fit any application - namely ArrayBuffer, TypedArray, and DataView.
We'll try to understand more about them by drawing comparisons with the real world, so please bear with my spectacularly unimaginative metaphors.
ArrayBuffer
We can think of our raw binary data to be a massive amount of all kinds of building material. To store this amount of material for any sort of further usage, we'd need a warehouse of the appropriate size. This warehouse is our ArrayBuffer.
ArrayBuffer is a representation of generic, raw binary data. It's a fundamental data structure for working with binary data in JavaScript (the term "byte array" is used in some other languages for similar data structures). An ArrayBuffer object is a reference to a fixed length, contiguous memory allocated in the heap. The binary data is generic and raw because -
Generic: It doesn't intrinsically have a particular data type. It just has a sequence of bytes and can store binary data corresponding to integers, unsigned integers, floats, strings etc.
Raw: The representation is similar to that in physical memory as there are no transformations internally
Array vs ArrayBuffer
ArrayBuffer is significantly different from Array in JavaScript (the Array.isArray() method returns false for buffers). It lacks the traditional .pop() and .push() methods because a buffer is initialised with a fixed length and is allocated a contiguous memory block which can't be pushed to or popped from - it can only be resized, but that too requires a deterministic max resize length on initialisation.
// buffer of length 16, can hold 16 bytes
const buffer = new ArrayBuffer(16)
console.log(buffer.byteLength) // 16Traditional arrays can hold any combination of different types of objects in them - string and number elements can exist in the same array, which is why often you won't get contiguous blocks of memory, unlike ArrayBuffer, where you do. Because the compiler/interpreter is getting information on exactly how much memory is being allocated and exactly how it's going to be viewed, it can make optimisations while working on the buffer. When iterating through that data, the compiler doesn't have to make calculated leaps through memory. Instead, it knows exactly how far to move ahead in memory to find the next data point. This sort of memory allocation and movement makes ArrayBuffer quite fast and optimised compared to traditional arrays.
TypedArray
Taking the previously drawn comparison further, if ArrayBuffer is the warehouse, then TypedArray are the series of carton boxes in which the building material is arranged and packed. These boxes could be of varying sizes - e.g. 100 boxes of 2 feet3, or 800 boxes of 1 feet3 and so on - but always of the same size at a time. The same building material in the warehouse can thus be arranged and moved in a series boxes of the same sizes. The underlying material remains the same, it's just viewed differently, in packing boxes.
In short, the two types of TypedArray are the 1 feet and 2 feet boxes, and we have access to a series of only one kind of box at a time.
Encoding and representation
Coming back to JavaScript land, TypedArray is a set of Array-like objects that allow you to interpret the underlying array buffer and work with binary data in a specific format. They don't actually store any data, they're a "lens" to make sense of the raw binary data, and these lenses comes in various shapes and sizes -
Int8Array - 8 bit signed integers, where every byte is an integer.
Uint8Array - 8 bit unsigned integers, where every byte is an integer.
Int16Array - 16 bit signed integers, where every 2 bytes is an integer.
Uint16Array - 16 bit unsigned integers, where every 2 bytes is an integer.
Int32Array - 32 bit signed integers, where every 4 bytes is an integer.
Uint32Array - 32 bit unsigned integers, where every 4 bytes is an integer.
BigInt64Array - 64 bit signed integers, where every 8 bytes is an integer.
BigUint64Array - 64 bit unsigned integers, where every 8 bytes is an integer.
Float16Array - 16 bit floating point numbers, where every 2 bytes is a floating point representation.
Float32Array - 32 bit floating point numbers, where every 4 bytes is a floating point representation.
Float64Array - 64 bit floating point numbers, where every 8 bytes is a floating point representation.
We needn't worry though, this isn't supposed to be memorised - let's understand what all this actually means. Consider Uint8Array and Int8Array:
Uint8Array - The U stands for unsigned, so this representation will have non-negative values only. The 8 means that the numbers will be stored in 8 bits (1 byte) and in the binary number system that means the range is from 0 to 28 -1 or 0 to 255.
Int8Array - This representation will have signed integers. The 8 means that the numbers will be stored in 8 bits (1 byte), but since this is a signed representation, the most significant bit (MSB) will be utilised in denoting a negative/non-negative value. Since one bit is used up, only 7 bits remain for the binary number system, which means the range is from -27 to 27 -1 or -128 to 127.
Other integer arrays behave in the exact same manner with increasing bytes needed to store the representation. Floating point arrays arrange the numbers according to the IEEE floating point format:
Float16Array uses 10 bits for the mantissa, 5 bits for the exponent and one bit for sign.
Float32Array uses 23 bits for mantissa, 8 bits for the exponent and one bit for sign, and so on.
// buffer of length 16 - holds 16 bytes
const buffer = new ArrayBuffer(16)
// unsigned int32 view over the buffer
const view = new Uint32Array(buffer)
console.log(Uint32Array.BYTES_PER_ELEMENT) // 4, each number takes up 4 bytes
console.log(view.length) // 4, count of numbers/elements
console.log(byteLength) // 16, size in bytes of the underlying bufferWe can also create views over a section of the ArrayBuffer instead of the whole thing by optionally specifying an offset and a length. No offset means the view covers the buffer from the beginning, and no length means the view covers till the end of the buffer.
const buffer = new ArrayBuffer(16)
const view = new Uint32Array(buffer, 4, 3)
// the offset is 4 - view starts from the 4th byte
// the length is 3 - length of the underlying buffer equivalent to 3 elements, which makes it (3 * Uint32Array.BYTES_PER_ELELEMT) bytesPlaying with binary numbers
Let's try to play around with different TypedArray views with the same ArrayBuffer data underneath to see what different representations look like for the same binary data.
const uint8View = new Uint8Array([250, 250, 250, 250, 250, 250, 250, 250])
const buffer = uint8View.buffer
console.log(buffer.byteLength) // this outputs 8, same as the Uint8Array lengthThe above snippet automagically creates a buffer underneath filled with the raw binary data represented by the typed array.
console.log(uint8View[0]) // this outputs 250
console.log(uint8View.length) // this outputs 8Here, each element (unsigned integer) of the view is 250, taking up 8 bits or a single byte. This view has 8 elements, 1 byte each.
const uint16View = new Uint16Array(buffer)
console.log(uint16View[0]) // this outputs 64250
console.log(uint16View.length) // this outputs 4Here, each element (unsigned integer) of the view is expected to be 64250, taking up 16 bits or 2 bytes. This view has 4 elements, 2 bytes each.
To visualise how exactly this difference arises between the two representations over the same byte data, let's convert the base 10 numbers in both typed arrays to binary.
250 = 11111010 (8 bits)
64250 = 1111101011111010 (16 bits)
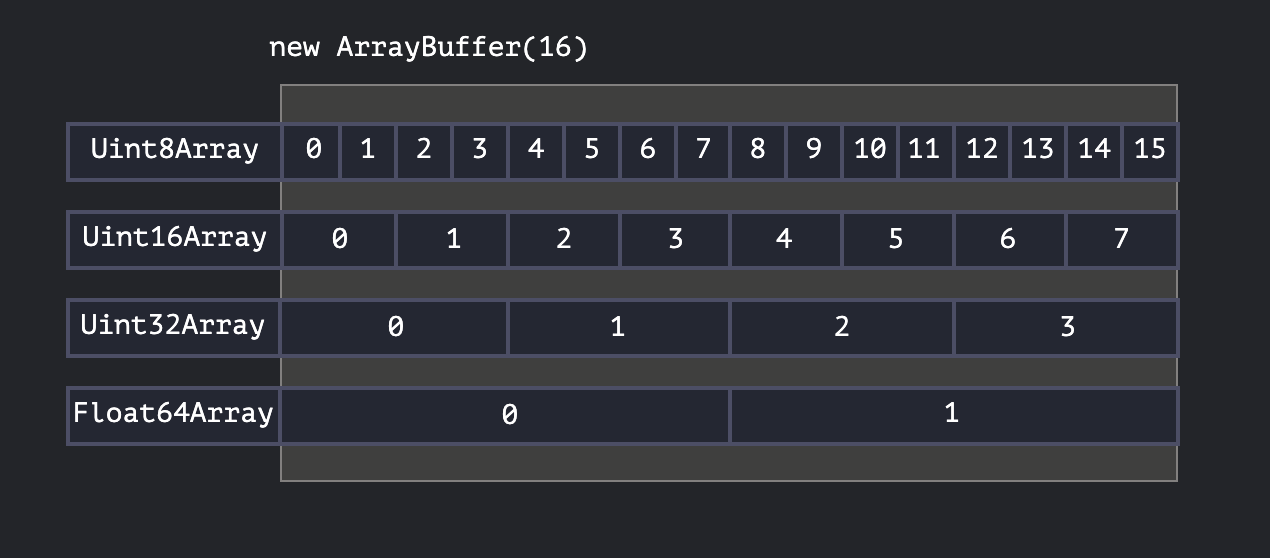
The Uint8Array treats elements as 8 bit numbers occupying 1 byte, and Uint16Array treats elements as 16 bit numbers occupying 2 bytes. So the arrays would look something like this in respective views (for visualisation purposes only):
uint8View = [ 11111010, 11111010, 11111010, 11111010, 11111010, 11111010, 11111010, 11111010 ]
uint16View = [ 1111101011111010, 1111101011111010, 1111101011111010, 1111101011111010 ]
The pattern seems obvious now. Appending the binary elements and their neighbours in the Uint8Array into a single 2 byte number yields us the element for Uint16Array
11111010 ++ 11111010 = 1111101011111010 (appending binary numbers)
which, converted to base 10, yields the result 64250.
So we see how the same underlying buffer can be represented in multiple ways depending which type we're using to view the data. It could be a representation of many small integers or a fewer count of larger integers. Or it could be a floating point number representation entirely. There's a really nice illustration on MDN that puts this into perspective.
Handling overflows
What would happen if we try to write a value into the typed arrays that is larger than its supported range? Let's try to put 256 and 260 as values in the Uint8Array view, which are out of bounds values since the supported range is 0-255.
const view = new Uint8Array(8)
const oobNum1 = 256
const oobNum2 = 260
console.log(oobNum1.toString(2)) /// this outputs 100000000, binary number
console.log(oobNum2.toString(2)) /// this outputs 100000100, binary number
view[0] = oobNum1
view[1] = oobNum2
console.log(view[0]) /// 0
console.log(view[1]) /// 4Nothing breaks, but extra bits seem to be cut off. For instance, the binary for 256 is 100000000 which is 9 bits but Uint8Array only allows for 8 bit per integer. For out of bounds numbers the less significant bits, the rightmost bits (this depends on the endianness of the system), are retained and the remaining are dropped.
So for 256, the 8 less significant bits are kept and the MSB is dropped, which leaves the value to be 00000000 which is 0. Similarly, the binary for 260 is 100000100. Again, the 8 less significant bits are kept and rest are dropped, so the remaining binary number is 00000100 which is 4.
Mathematically, the number's modulo 28 is preserved and the rest is dropped. We can think of this as the numbers wrapping around to the beginning of the range once they go beyond 255, and start from 0 again.
DataView
The warehouse metaphor might be going a bit too far at this point, but we’ll roll with it. We can think of a DataView as us having access to a series of all different kinds of boxes at the same time. The material in the warehouse can be packaged on demand in boxes of any size at the same time. For instance, 50 boxes of 2 feet3 and 400 boxes of 1 feet3 at the same time to pack the warehouse material instead of having access to a sequence of just a single type of box size.
DataView is a special type of "untyped" view over ArrayBuffer that gives more flexibility to work with binary data than a TypedArray by allowing data access at any offset, in any format, and in a specifiable byte order.
In case of TypedArray the constructor dictates the representation of the underlying binary data, whether its signed, unsigned, 8 bit, or 16 bit etc. DataView is more flexible and exposes methods that allow for choosing the representation format at runtime. e.g. getUint8() and getUint16().
DataView is great for use cases where the same buffer has mixed format data stored in it. This is a common occurrence in network programming where data passing in protocols happens in buffers where, for instance, n bytes in a buffer specifies the length of the entity for the next m bytes, and both n and m are read in different representations.
For instance:
// this creates a buffer with the specified binary numbers
const buffer = new Uint8Array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]).buffer
// syntax for initialising data view
const view = new DataView(buffer)
console.log(view.getUint32(0, true)) // 67305985 -> 32-bit number, first 4 bytes
console.log(view.getUint8(4, true)) // 5 -> 8-bit number, 1 byteAnother way to do this with TypedArray instead:
// this creates a buffer with the specified binary numbers
const buffer = new Uint8Array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]).buffer
const uint32View = new Uint32Array(buffer, 0, 1)
console.log(uint32View) // this logs -> Uint32Array(1) [ 67305985 ]
const uint8View = new Uint8Array(buffer, 4, 1)
console.log(uint8View) // this logs -> Uint8Array(1) [ 5 ]This is of course a very simplistic example of binary data manipulation but the point here is that DataView has powerful methods exposed that allow accessing and manipulating binary data in different formats in a single view. This can be very useful while passing binary streams across systems and decoding them on the application side if the data is composed of different sections which hold information like content length and offsets about other sections in the same stream. Network protocols often use this methodology to encode information in packets and headers - we too use a similar strategy in our app to receive and decode binary information for image processing use cases.
Endianness
Endianness refers to the order in which a computer reads bytes. Like how English is read from left to right and Urdu is read from right to left, computers read bytes either from left to right or from right to left. The two most common orderings are -
Little endian: This order stores the MSB (most significant bit) last. In other words, the bytes are stored in least-to-most significant order, with LSB occupying the smallest memory address.
Big endian: This order stores the MSB first. In other words, the bytes are stored in most-to-least significant order, with MSB occupying the smallest memory address.
There was an example of this a few sections above where we discussed how the same binary data was expressed as a Uint8Array with 8 numbers being 250 vs a Uint16Array with 4 being 64250. In that example, we were representing 250 as 11111010 and 64250 as 1111101011111010 - this representation has the MSB first ("first" essentially means occupying the lowest address) while reading them, and such byte ordering is big endian. Conversely, if we were to represent 250 as 01011111 and 64250 as 0101111101011111, the byte ordering would have been little endian since the MSB is read and stored last ("last" essentially means occupying the highest address).
The ordering here doesn't affect the value of the element itself in any way, it just affects the order of storing and reading the byte data by the processor from the registers. So for all intents and purposes, the binary output that you will get in your system after binary manipulation will be unchanged, but the ordering of bits and their arrangement in registers will differ for different endianness.
The systems that we use on a daily basis to write programs are mostly little endian. x86 architecture is little endian, ARM architecture supports both orderings but is predominantly used as and defaults to little endian. Big endian ordering is mostly used in network protocols - TCP is big endian according to its spec.
Byte ordering doesn't concern us much as long as the application is dealing with binary data within the system - every system is a black box that is self sufficient in handling its respective endianness. Byte ordering starts mattering when systems with different endianness start communicating or when systems have to deal with bytes coming over the network. DataView gives us a convenient way to control the endianness while reading/writing bytes to a buffer. TypedArray views are in the native byte order always but DataView getter/setters allow us to change that. In the examples above -
console.log(view.getUint8(4, true))The true parameter tells the DataView to read the data in little endian order, otherwise it defaults to big endian.
Conclusion
This article was an attempt at explaining and differentiating between different constructs that JavaScript exposes to allow us to read and manipulate binary data efficiently (albeit "efficiently" is a loaded word when dealing with JavaScript) for practical use cases in applications dealing with image processing, graphics, networks, communicating data to the GPU and many more.
Thanks for tuning in!
Bonus read
There's a great article on how the v8 team at Google improved the underlying performance of DataView to match with TypedArray. While these abstractions are provided by JavaScript, we often take for granted the work that goes into making these performant in JS engines, and by extension our browsers and Node environments.
Give it a read! https://v8.dev/blog/dataview




:clap:
Good stuff! Very informative